Why Equal Temperament?
The picture to the right shows the lattice of fifths and thirds, a map of untempered harmonic space, extending to infinity. The map shows how to venture farther and farther from home, the tonic, and stay perfectly in tune no matter how far you roam.
Every single note in this infinite matrix is tuned to a different pitch. You can go out to Mars and beyond, and you will never see the same note twice.
In pure vocal music, this is not as hard as it seems. The voices will tune up to each other, and it’s natural to sing the pure intervals. So if the piece makes its way to the far north, by small steps, the voices may be singing something like a #3, #7 and ##5, and it will be a nice pure major chord.
Want to hear this in action? Here’s a video of a piece by Guillaume de Machaut. I find this music exhilarating. Check out the astonishing note at 3:00. It’s not jazz, not classical, not blues, it’s adventurous harmony on the lattice of fifths and thirds.
In the 1300’s, before temperament started taking over in Europe, there was a flourishing of untempered music, both secular and spiritual, called Ars Nova. Machaut was one of the greatest composers of that era. In Harmonic Experience, Mathieu shows a map of a Machaut piece that wanders amazingly far on the lattice, staying in tune all the way.
The only instruments that can really play like this have infinitely variable pitch. Voice is top dog, although the fretless stringed instruments can do it too (standup bass, violin, etc).
For instruments of fixed pitch, such as pianos, organs, guitars, lutes and accordions, the tuning of the lattice in just intonation is an absolute nightmare. How do you accommodate all those pitches? The keyboard to the right gives it the old college try. (Photo is from a gallery of such keyboards at H-pi Instruments.) Yipe! ltbb_035-44k
Fixed pitch instruments work just fine if you stay in a small part of the lattice, and stay in one key. But after Ars Nova, European composers and listeners got more and more interested in wandering the map, and in changing keys, or modulation. So they started to look for compromise tunings, in which one note could represent several nearby ones, close enough in pitch that the ear would tend to interpret them as the pure note.
For example, there are two major seconds on the inner lattice. In just intonation, the 2 (ratio 9/8) is tuned to 204 cents. The other major second, 2- (ratio 10/9) is tuned to 182 cents. If the major second on your instrument is tuned to, say, 193 cents, it will be right in the middle and you can use it to play both notes, slightly but perhaps acceptably out of tune.
There are many possible ways to “temper” the scale, and each one compromises different notes. Over the next few hundred years after Ars Nova, tunings evolved through a bunch of meantone tunings, which detuned fifths and left thirds quite pure, through well temperament, which spreads out the detuning enough that it becomes possible to play in all keys. During this lattice study I discovered, to my surprise, that Bach’s Well-Tempered Clavier was not written for equal temperament. In ET, all keys sound exactly the same, but if Bach is played in the original tuning, each key sounds slightly different. Such key coloration was an integral part of the music, and composers took it into account.
Finally, by the last half of the 1700’s, equal temperament had become pretty much standard.
Twelve-tone ET completely flattens out the lattice, so that each block of twelve tones (the different colors in the top picture) is tuned exactly the same. It’s sort of like a map projection, in which the the geography is slightly distorted so that the curved surface of the earth can be represented on a flat page. In ET, the fifths are very much in tune (only off by 2 cents), and both major and minor thirds are considerably compromised (off by 14 and 16 cents respectively, quite audible). The minor seventh (Bb in the key of C) is the farthest off of the ET notes, 18 cents. Click here to hear the JI and ET minor sevenths compared.
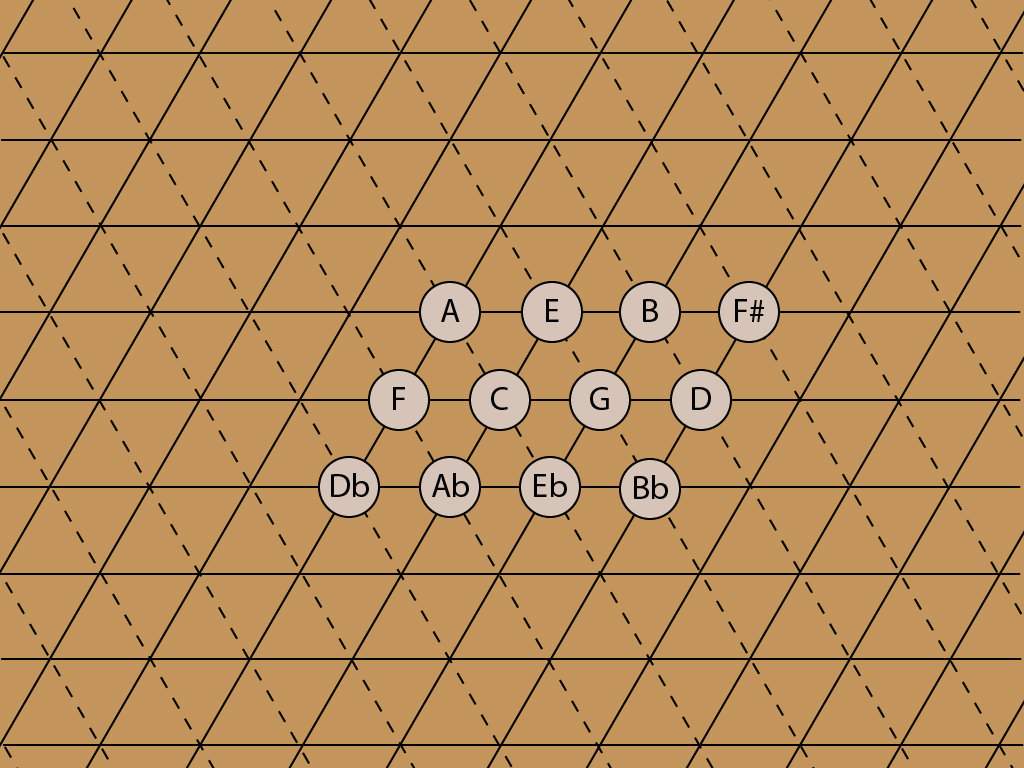
This is how the central portion of the lattice looks in equal temperament (in the key of C):
Whew! Familiar territory. There’s the tonic major chord, C-E-G, and the relative minor, A-C-E, and so on, and it’s easy to see how they relate to each other.
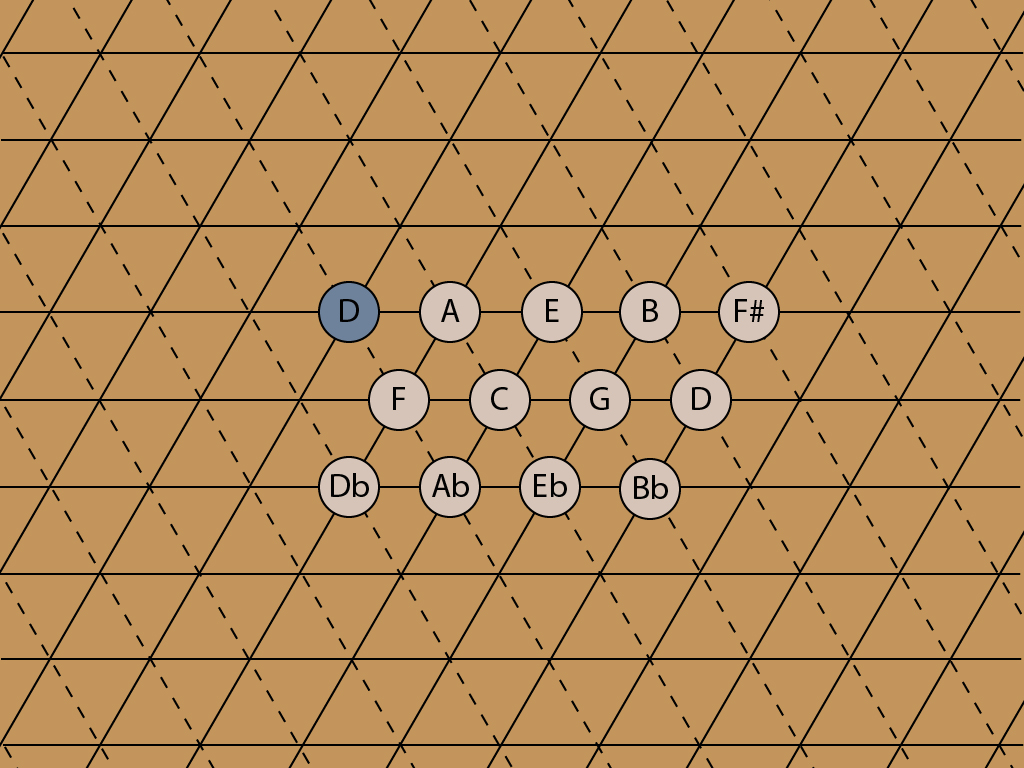
When you start expanding the ET lattice, it’s a simple repeat. Starting with the 10/9 major second:
No pesky commas, it’s just another D. Note that a new chord has appeared, the minor chord on the second degree of the scale — D-F-A, called the ii chord and very common in jazz. Here’s the whole lattice, converted to ET.
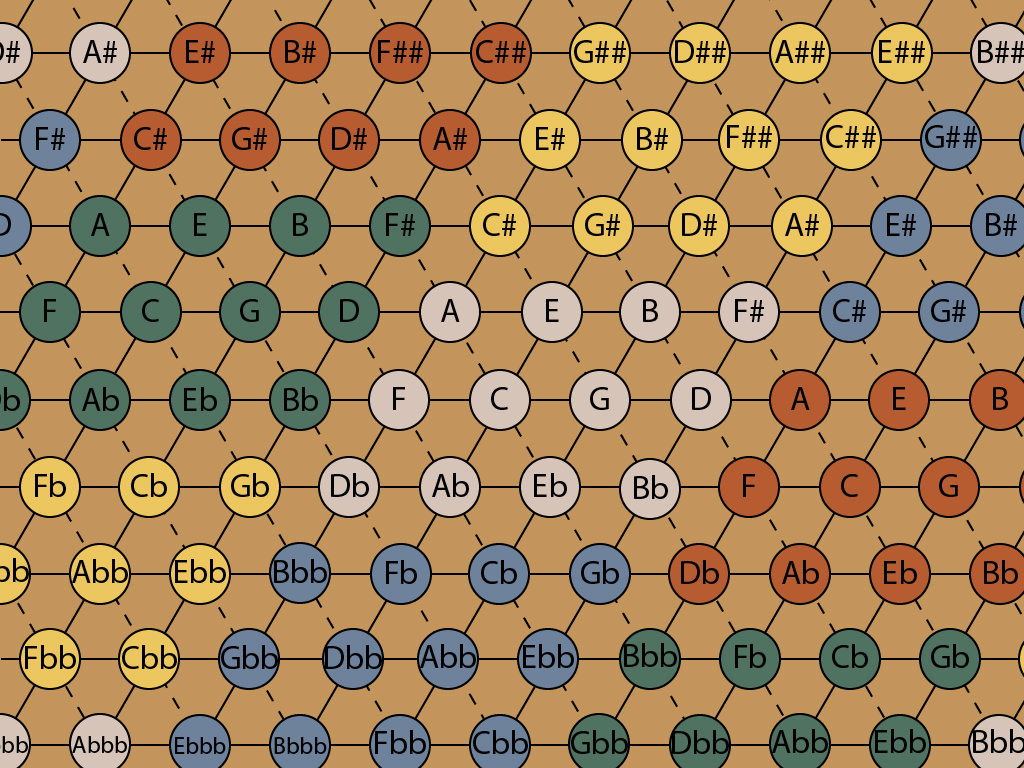
Now the blocks repeat exactly. Think of the lattice as a horizontal surface, extending to the north, south, east and west, and imagine the pitch of the notes as the vertical dimension. The untempered lattice has a tilt to it — up to the east and down to the west, by 22 cents per block, and down to the north, up to the south, by 41 cents per block. The equal tempered version is flat. You can wander at will, and play everything with just 12 pitches.
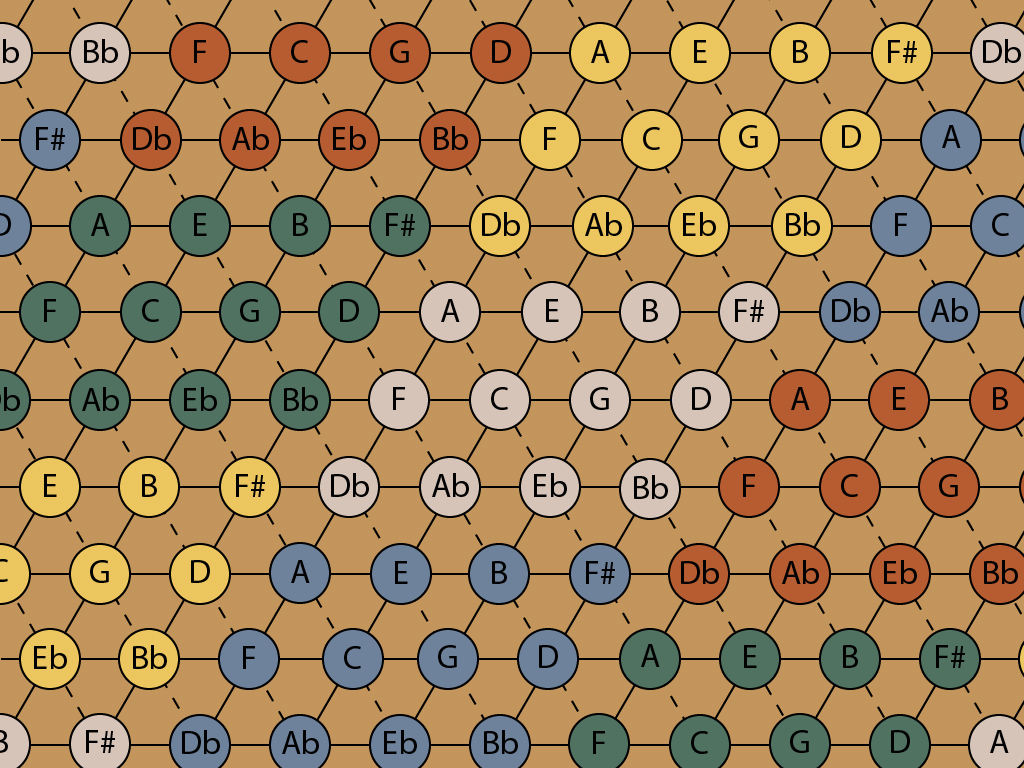
I oversimplified the ET names in order to show the repetition. For example, in the yellow block just north of the center, Ab really should be G#. In ET, these are exactly the same in pitch, but calling the yellow one G# helps in understanding where it is on the lattice and how it might be used in a composition. The following lattice shows a more informative way to name the ET notes. The pitches of the notes in the blocks are still exactly the same — 100, 200, 300 cents and so on. A C## is just the same as a D, in equal temperament. The same in pitch, but not in function.
This lattice explains why classical music has such oddities as double flats, double sharps, and weird notes such as E#. Why not just say F? E# and F are tuned the same, but they are in different places on the lattice, and if you see an E#, you know you’re in the northern zone.
Beethoven, who helped usher in the Romantic period, used equal temperament to roam the lattice like a wild tiger. Some of his music goes so far out on the map that quadruple flats appear. Click here for some crazy Beethoven stuff — the text is pretty dense but just look at the music notation!
Next: Rosetta Stone