The Infinite Lattice

The lattice goes on forever in every direction.

It starts with the tonic, the 1, the Big Bang of the musical universe.

Multiplying and dividing the tonic by 3 generates the horizontal axis. This is the familiar circle of fifths, although in just intonation, it doesn’t quite come out exact. If you multiply by 3, twelve times, you run through all of the scale degrees and land back on the tonic, 19 octaves up … almost. Three to the twelfth power, octave reduced until it’s back in the original octave, comes out to about 24 cents, not zero. Equal temperament flattens this out by subtracting two cents from every fifth. Very handy.

Multiplying and dividing by 5 generates the vertical axis. The two together create a plane, a map of harmonic space. Tonal music, that is, music that is organized around a key center or tonic, can be viewed as a journey on this map.

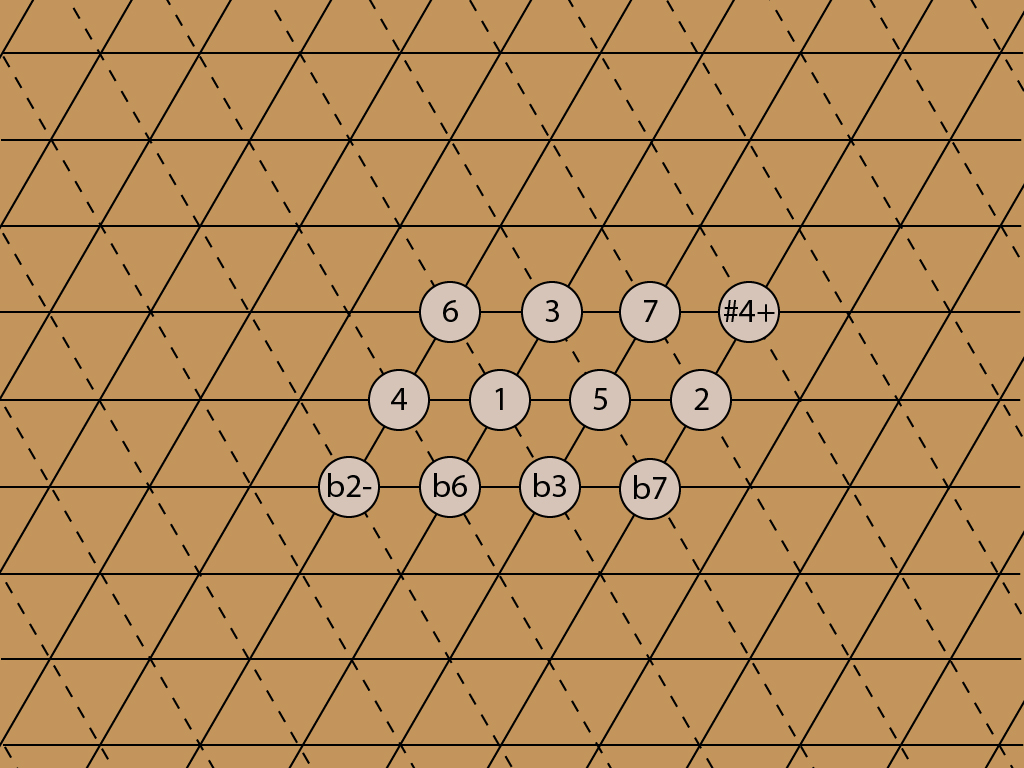
In the center of the map, there is a lovely pattern of twelve notes that form a chromatic scale.

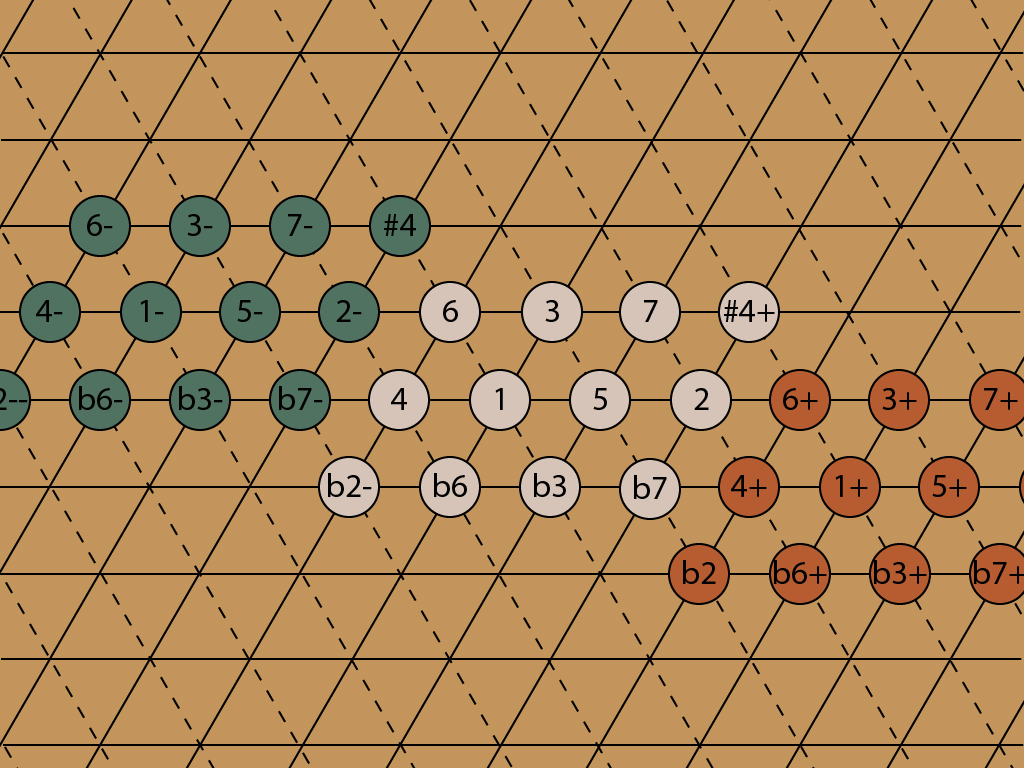
Each of these notes has a cousin, four fifths down and a third up, that is tuned almost the same. It’s 22 cents flat of the original note, a distance of a Didymic comma. Thus there is another major second, the 2-, just outside the 12-note pattern.

Doing the same thing for all twelve notes creates another chromatic scale to the west. It’s the same scale, 22 cents flat of the original. It works the other way too — there is another block of notes to the east, same scale, 22 cents sharp.

The other comma I’ve discussed, the Great Diesis, shows how to extend the lattice north and south. This one shifts the pitch by 41 cents. It’s the shift that results when you go up or down by three major thirds. Equal temperament flattens this comma out too, but the adjustment is more extreme. Every major third in ET has to be sharp by about 14 cents in order for three of them to add up to an octave, a noticeable difference in pitch.

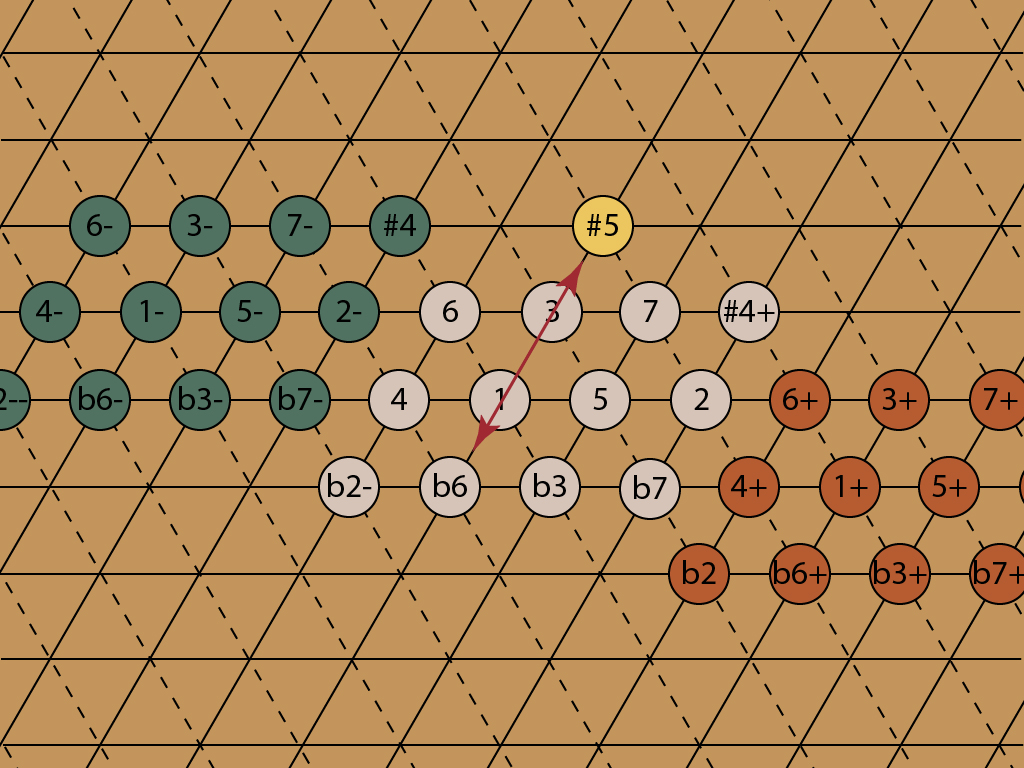
The pairs created by the Great Diesis have different note names. The b6 in the lattice above is at 814 cents, and the #5 is at 773 cents — 41 cents flat. In the key of C, these notes are Ab and G#, and they are played with the same black key on the piano, between G and A. Until I started studying just intonation and the lattice, I had no idea why one would want to think of these as different notes. It’s not an old-fashioned or obsolete distinction. It’s very useful, when writing or arranging, to know where you are on the lattice, and it’s just as useful in ET as it is in JI.

Now I can add two more blocks to the north and south.

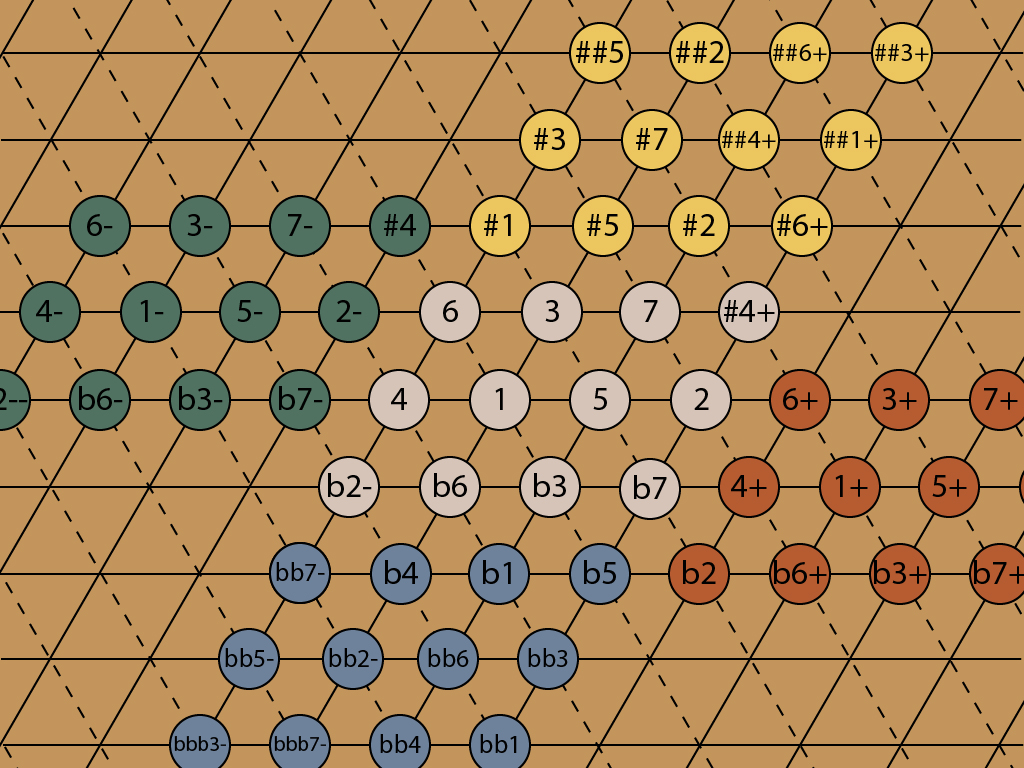
And here’s the whole thing. The colors are arbitrary.

The chromatic scale, a block of 12 notes, has tiled the plane. The note names get pretty crazy — triple flats indeed! But they exactly describe the pitch of every note, in just intonation. Start with the major scale, 1-2-3-4-5-6-7. Every sharp (#) adds 70 cents to the original note, and each flat (b) subtracts 70 cents. Each + adds a Didymic comma, 22 cents, and every – subtracts 22 cents.

Next: Why Equal Temperament?