Tonal Gravity and the Major Scale
In my last post, I proposed a simple way to graph tonal gravity against the octave.
Overtonal notes, generated by multiplying, are restful, stable — they have positive polarity, pulling toward the center. Reciprocal notes, generated by division, are restless, unstable — they push. I call this negative polarity. Mixed-polarity notes have both, and I’ve chosen to simply add their overtonal and reciprocal components together to get the total polarity.
Here again is the graph of the 13 most central notes of the lattice.
The stable notes are gravity wells, and the unstable ones are peaks. Melodies and harmonies dance in this gravity field. Higher points represent tension, lower ones resolution, and the lower they are, the more resolved and stable. The tonic major triad, most stable of all, occupies the lowest spots — 1, 3 and 5.
The polarity map of the major scale looks like this:
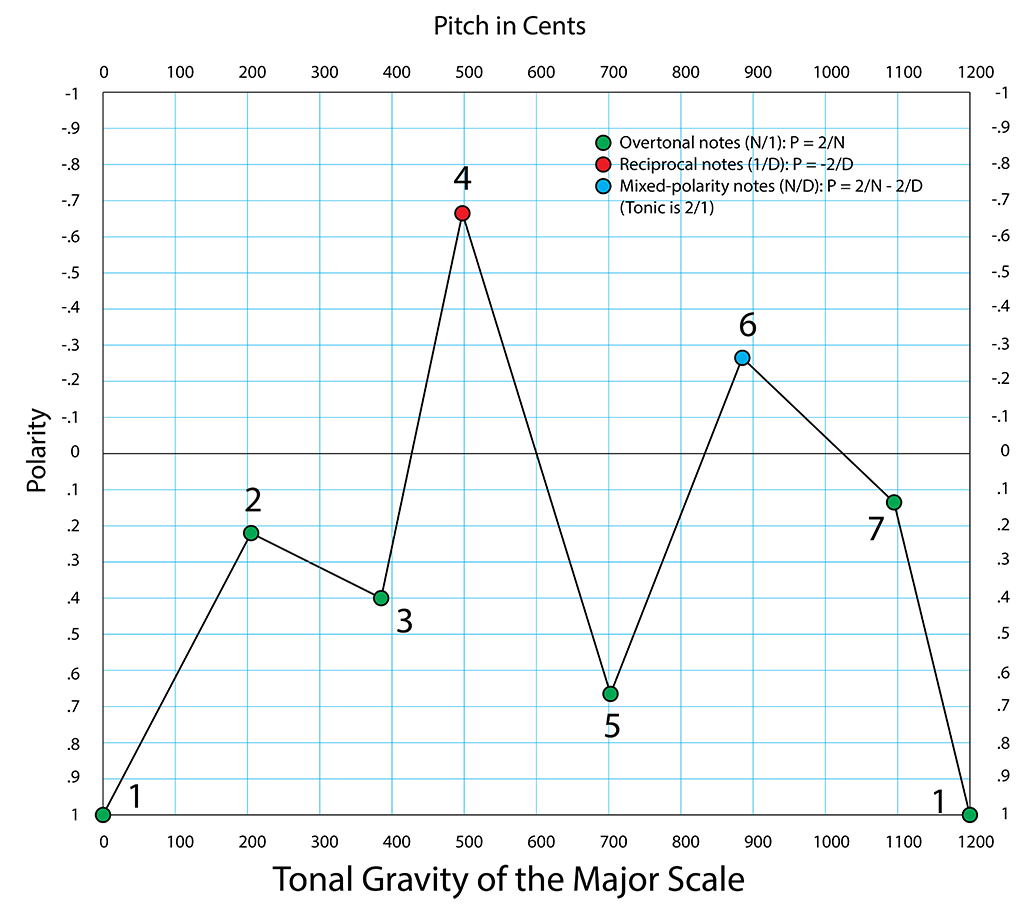The notes are all overtonal except the 4, which is strongly reciprocal, and the 6, which is mixed and slightly unstable.
Here’s a split screen video showing the major scale, against a tonic drone, on both the lattice and the octave. This is an example of how the lattice serves as a Rosetta Stone, a translator between harmonic and melodic space.
Can you hear the push/pull quality of the notes? Each note has its own feeling against the steady 1.
Next: A Theory of Everything
Hi Gary,
Interesting demonstration. What I find a little strange is that we are always taught that the octave is equivalent to the tonic, and therefore there is no tension. And I accept that to some degree. But could this be a case of simply rehashing what we’ve been taught to accept.
I don’t know if it’s just me, but if I sing up the scale to an octave and hold the octave note (singing out loud) while simultaneously impressing the sound of the tonic in my mind silently/mentally, I find a very strong pull back to the original tonic. It’s as if the octave is both a resting place and a scale degree with a very strong pull to the tonic. There is something strangely ambiguous about its harmonic tension. Do you sense it?
Interesting! I don’t strongly feel what you do, the octave feels like home too. But I do feel it a bit. The lower in pitch, the more “home-ish” it feels. Maybe it has to do with the harmonic series — lower notes are more likely to be the fundamental.
Is there a way to get a continuous curve for the entire 2:1 continuum? I imagine there’s some sort of calculus involved, and that you would see a fairly chaotic curve, but with clear nodes of stability.
It could be done on a spreadsheet. Devise a way to methodically list all possible ratios up to an arbitrary limit, and from the ratios you can calculate two columns, one for pitch in cents, and one for tonal gravity. Then an X-Y graph would give you a continuous curve.
If the limit gets too high, the low-ratio notes (3/2, 5/4 and so on) would become narrower and narrower spikes. The high-ratio notes will all be close to the x-axis. So there would probably be an optimum limit that is informative — above that, it would become mostly low-level static.
I’d be curious to see the result — let me know if you tackle it!
I carried this exercise out–the “continuous curve” is something I’ve been curious about for a while.
My conclusion is that the polarity formula is mainly of heuristic value for the area of the grid close to the tonic.
The problem is that you will easily get many values with large polarity as you zip along an axis in a mixed quadrant. For example, take the note with ratio 3/(5*5*5) = 3/125, which is not even that far out of the central grid you often consider. Then P = 1/3 – 1/125, which is within a whisper of 1/3, the polarity of the perfect fifth (and the highest possible outside octaves). However, this pitch is at 743 cents, quite a ways above the perfect fifth’s 702 cents and not very consonant.
Now reciprocate by another third, to 3/(5*5*5*5) or 3/625, for which P=1/3-1/625, which is even closer to the polarity of the major third–but the pitch of this note is at 357 cents, a dissonant flat version of the major third. The actual untempered major third has a lesser polarity P but is much more consonant.
By continuing to reciprocate by thirds, you get pitches all over the scale but all with polarity P very close to that of the perfect fifth.
Another example is to proceed 13 spots in the overtonal fifths direction. The ratio will be 3^13/1, for a polarity P very close to 0. However, this pitch is only 23 cents off from the perfect fifth (this is why ET works). A sensitive ear will perceive some dissonance, but it’s not so far off that it shouldn’t have a high polarity close to the 0.67 of the perfect fifth.
I think your values give a good feel for the polarity close to the tonic on the grid, but they don’t hold farther away. I’m continuing to try to come up with some general gravity measure.
I agree with you on all counts. The more points on the curve, the more “hashy” it looks, and resonance becomes meaningless at larger ratios. Keep me posted as you search for something more general!