Putting Some Numbers on Tonal Gravity

I believe the sensation of tonal gravity is the most important driver of tension and resolution in tonal music, music that has a central key note.

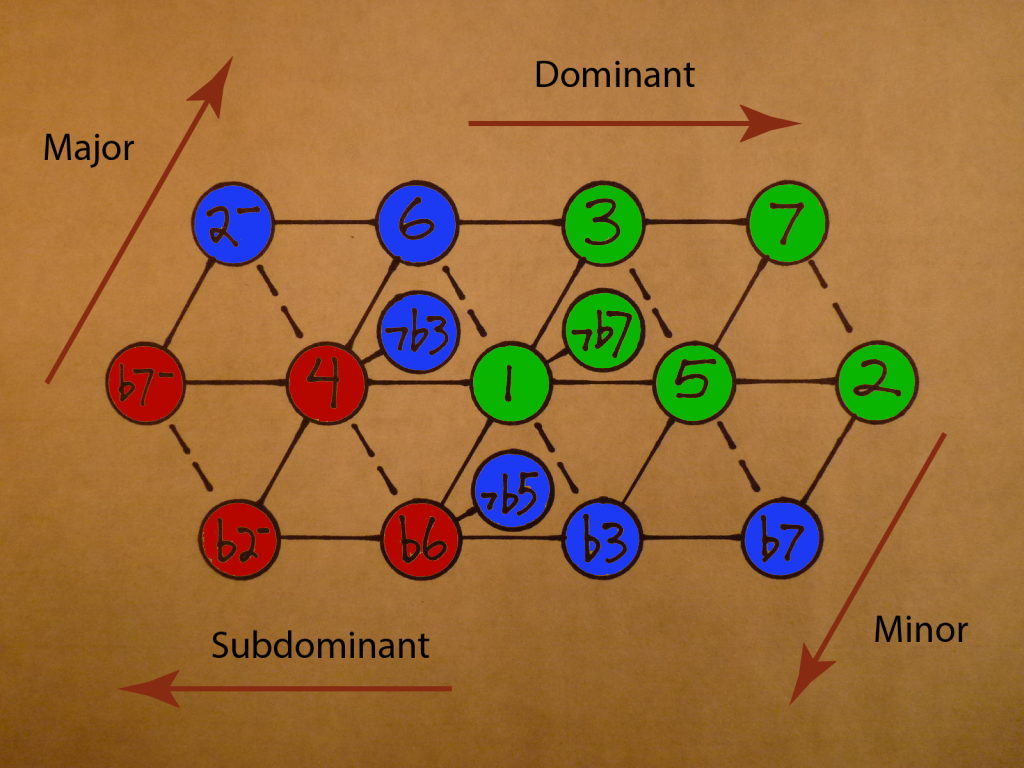
The tonic is like a sun, creating a gravitational field around it. The lattice is a beautiful map of this gravitational field, in harmonic space.

Tonal gravity acts like real gravity, in that it’s strongest close to the center. The farther out you get, the weaker the effect.

There is a difference, though — unlike physical gravity, which only attracts, tonal gravity has two polarities — it can attract or repel. Briefly, if an interval is generated by multiplication, it will pull toward the tonic, as though to say, “You’re going the right way, you’re just not there yet.” If the interval is generated by division, the sensation is more of a push — it still points to the tonic, but now it’s saying “It’s over that way, go!”

Overtonal notes are stable, reciprocals are unstable. Reciprocal intervals create tension, overtonal ones create resolution.

The article on Polarity goes into detail, with examples.

The lattice can be divided into four quadrants, each with a characteristic tonal gravity. The northeast quadrant is entirely overtonal. This is the world of Major/Dominant: overtonal thirds, overtonal fifths.

The southwest quadrant is entirely reciprocal. Every interval is generated by division.

The northwest and southeast are zones of mixed polarity, overtonal on one axis and reciprocal on the other one. Here’s a map of the quadrants and the compass points:

Green is overtonal, stable, tonal gravity pulls.

Red is reciprocal, unstable, tonal gravity pushes.

Blue is mixed, gravity pulls on one axis and pushes on the other.

For a couple of years now, I’ve been chewing on how to represent the tonal gravity of the lattice mathematically. To describe what I experience, the equations should behave as follows:

1. Overtonal intervals have one polarity, and reciprocals have the opposite polarity,
2. Gravity gets weaker the farther one gets from the center, and
3. Multiplying or dividing by 2 does not affect tonal gravity. This is to account for the octave phenomenon — going up or down an octave does not change a note’s position on the lattice.

Here’s my latest approach. I’m not presenting this as some kind of truth — but it nicely matches my own perceptions, and it leads to some interesting graphs. Any input you may have is welcome — feel free to comment, or email me from the Contact page. Here goes:

I will call the direction and magnitude of the tonal gravity field P, for Polarity.

Intervals are expressed as a ratio of two numbers, numerator and denominator, N/D. For example, a perfect fifth is 3/1, or N=3, D=1.

1. For purely overtonal notes, of the form N/1: P = 2/N.
2. For purely reciprocal notes, of the form 1/D: P = -2/D.
3. For compound notes, with both overtonal and reciprocal components, add the overtonal and reciprocal gravities together: P = 2/N – 2/D.
4. The ratio of the tonic, the 1, is 2/1.

I’d better explain that last one, because it would seem at first glance that the ratio of the tonic would be 1/1.

But what is the actual tonic? It has no specific pitch. It is not a ratio. It is an abstraction, the anvil upon which all notes are forged, the sound of one hand clapping. If a song is in the key of A, all of the A’s from subsonic to ultrasonic are actually octaves of the tonic, created by multiplying by two. It is impossible to say that any one of these A’s is “the” tonic — the tonic is “A-ness,” that thing which connects the numbers 110, 220, 440, 880, to infinity in both directions. I submit that the “1” of the lattice, which is a real pitch (or set of pitches, an octave apart, just like all the other notes) is in fact the octave, and its ratio is 2/1.

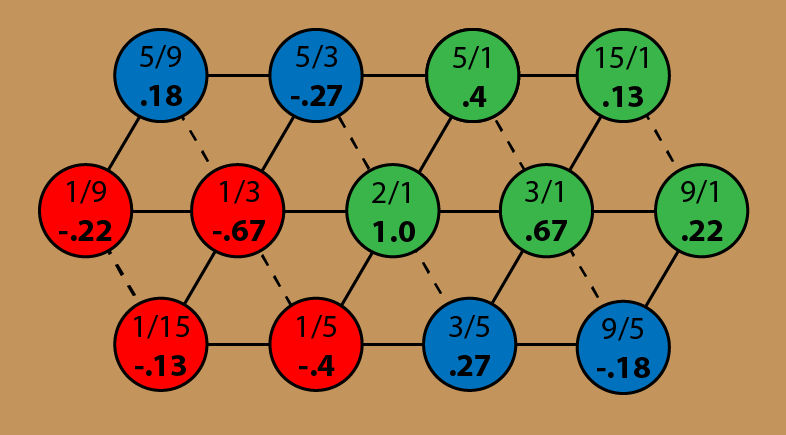
Here’s another drawing of the inner lattice. Instead of the note names, I’ve filled in the ratios, and the value of P.

The green notes all have positive polarity, getting weaker as they get farther out. The red ones have negative polarity, also fading with distance. The blue ones have different polarities. Sometimes the overtonal part dominates, sometimes the reciprocal.

The b3, just southeast of the tonic, is a mixed-polarity note. Its ratio is 3/5, combining an overtonal fifth, P = .67, with a reciprocal third, P = -.40. If I just add the two gravities together, I get a positive net polarity of .27.

This makes sense. The minor third is considered to be a stable interval, though not as stable as the major third.

Both the major and minor triads consist entirely of stable intervals with positive P, which helps explain their special place in music.

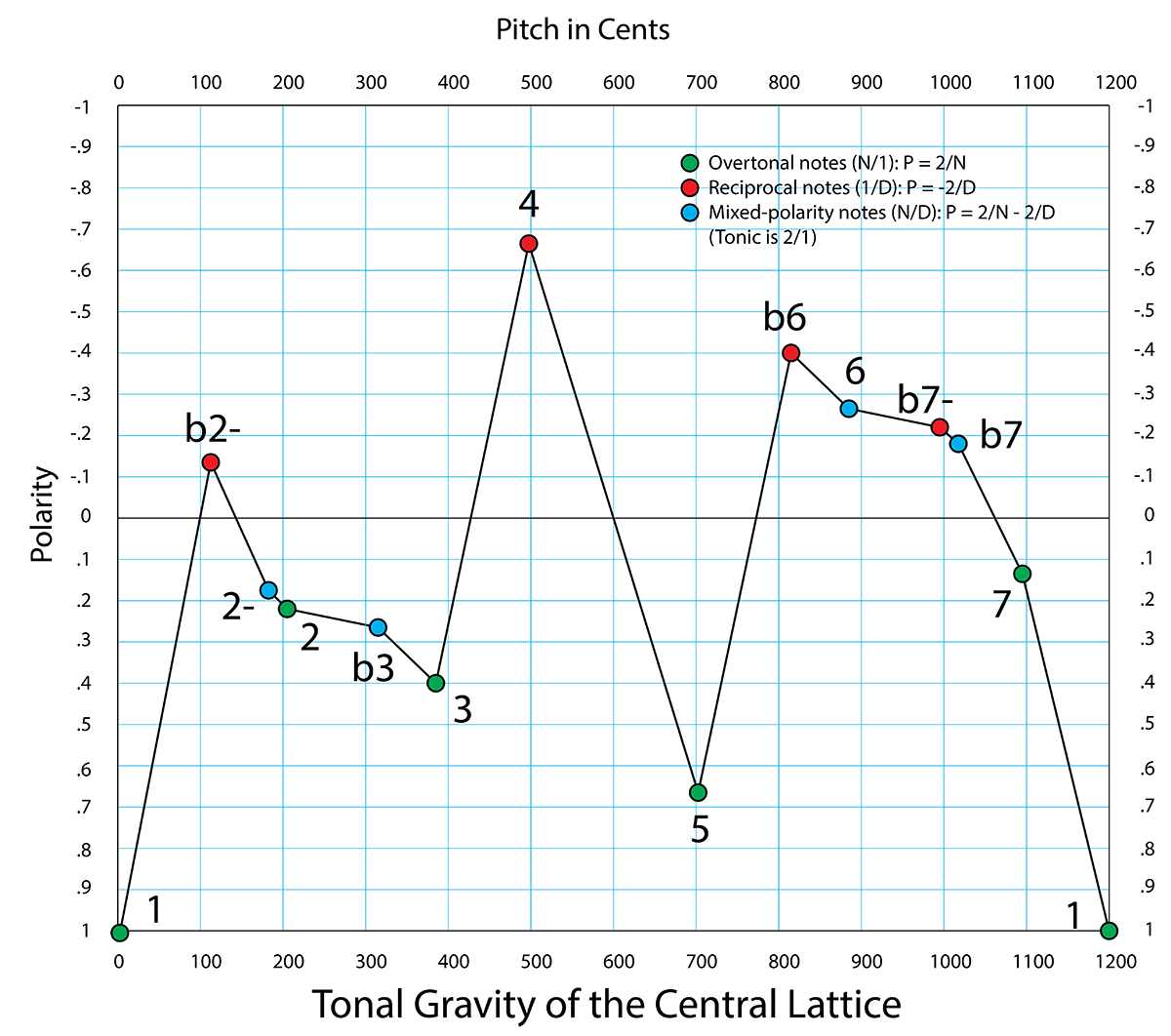
So: now that I have some values for P, I can graph the tonal gravity of these 13 inner notes against the octave, in order of pitch.

Positive polarity is at the bottom, so that the feel is the same as real gravity. Unstable notes are up on mountain peaks, and when they resolve to stable ones they slide down into the gravity wells of the stable notes.

There is that tasty melody zone I mentioned a few posts back. The whole region from 2- to 3 is stable.

The 4 is an isolated peak, and it’s easy to imagine a 4 sliding into the pocket of the 3, or the 5. This is what happens when a Sus4 chord resolves.

The 7 is lightly stable but hanging on by its fingernails — it’s called the leading tone, because it “wants” so badly to resolve to the 1. The tonal gravity of the 7 is usually thought of in terms of melodic pull — here’s a graphic demonstration that it has harmonic pull as well.

There is an unstable region from b6 through b7, with all the mirror twins of that stable melody zone. A melody will sound unstable, unresolved as long as it stays in that region.

This is the gravitational field in which the music moves, a sort of tonal skate park.

Next: Tonal Gravity and the Major Scale