Another Comma

One more comma shows up in the central portion of the lattice.

In equal temperament, three major thirds adds up to an octave. The major third is an interval of four piano keys (out of 12) or 400 cents. Three of them is 1200 cents, exactly an octave.

In just intonation, this is not the case. The 5/4 major third is a narrower interval, 386.3 cents. Adding three of them together gives 1159 cents, 41 cents shy of an octave.

On the lattice, a stack of major thirds looks like this:

Every three places, the notes repeat — almost.

One such pair is the b6 and #5. In the key of C, they would be an Ab and a G#, and on the piano you would play them both with the black key between G and A.

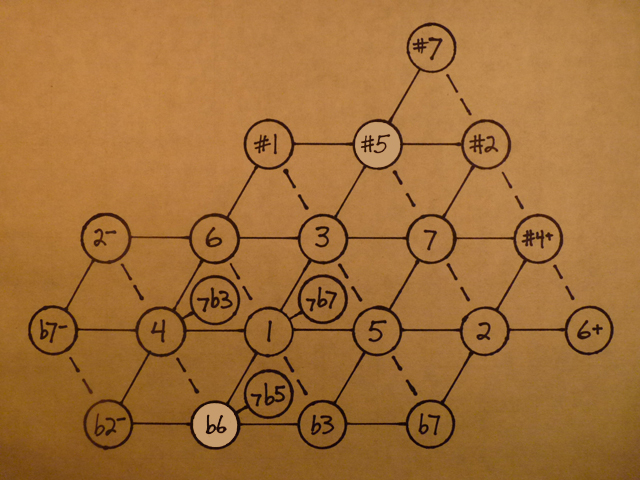
In just intonation, the b6 is the ratio 8/5, which works out to 814 cents, and the #5 ratio is 25/16, which is 773 cents, almost a quarter tone flatter. (I describe cents and how to calculate them here.) The 41-cent distance between these two notes has several names. Mathieu’s is my favorite: Great Diesis (Dye-uh-sis).

Its formula is x5, x5, x5.

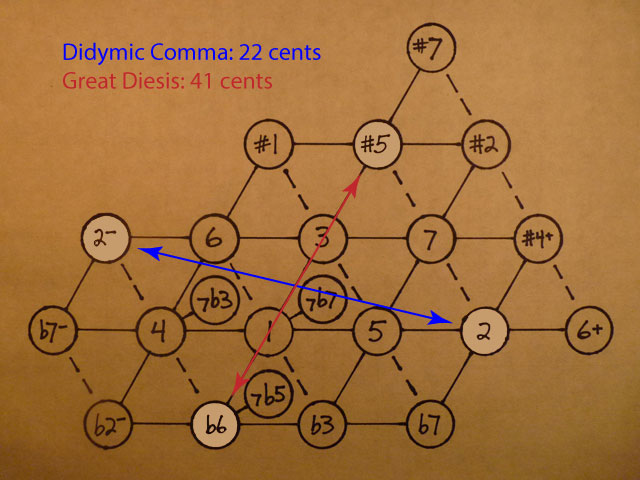
The reason I’m introducing these commas is to show how the lattice repeats itself. Here are the two commas on one lattice:

The lattice extends infinitely in the horizontal direction, and every time it repeats, the pitch shifts by 22 cents. It also repeats in the vertical direction, shifting by 41 cents with every repetition.

Next: The Infinite Lattice