Three Flavors of Seventh Chord
Chords and other collections of notes have consistent, recognizable shapes on the lattice. A major chord is a triangle sitting on its base, a minor chord is a triangle on its point. Yesterday’s post has videos showing these chords.
In the songs I know and write, the next most common chords after major and minor triads are seventh chords.
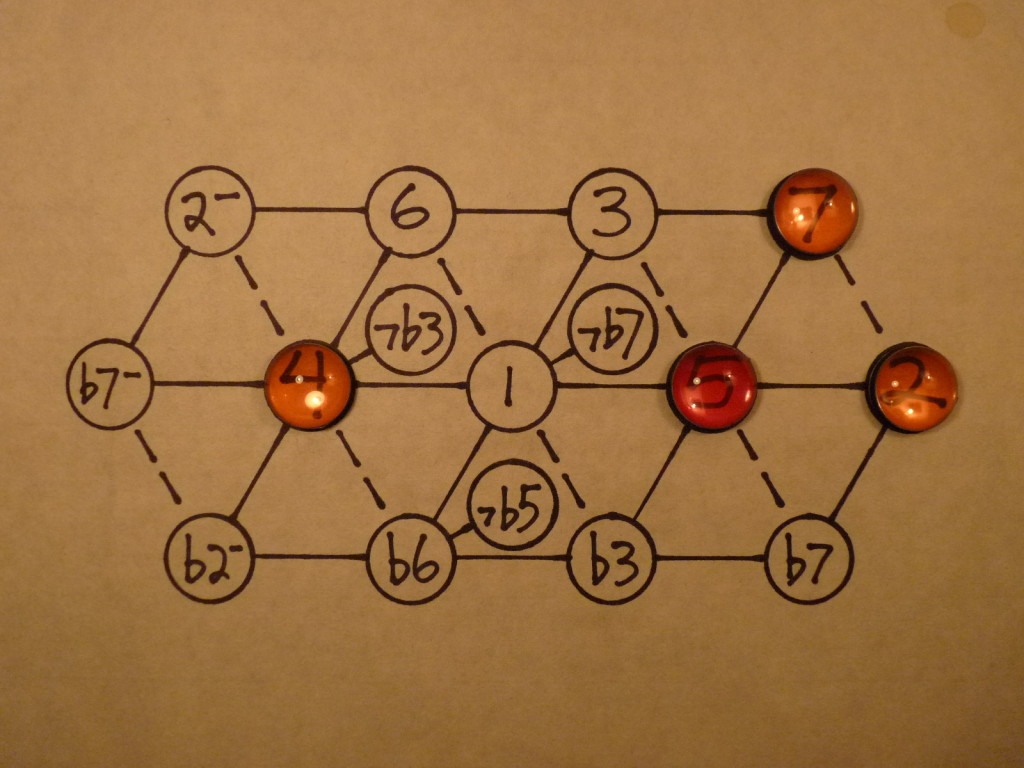
By convention, a “seventh chord” means a triad, with a minor seventh added. If the added seventh is a 7, or major seventh, it’s called a “major seventh” chord.
A minor seventh is an interval of ten half steps, or two shy of an octave. There are three different minor sevenths in the inner lattice, and each one makes chords with a different sound and function — that is, if you are playing in just intonation, or untempered. In equal temperament, the minor sevenths all sound the same, but there is still profit in knowing that they are different, because they function differently in chord progressions.
The three notes are:
- The b7, at 1018 cents. The ratio is 9/5.
- The b7-, or dominant-type seventh, at 996 cents. The ratio, octave reduced so it lands in the same octave as the tonic, is 16/9.
- The 7b7, at 969 cents. This is 7/4, the harmonic, or barbershop seventh, a consonant note that appears in the actual harmonic series of the tonic.
Here are some movies in just intonation, so you can hear the differences.
————————————–
First, the b7, added to a minor chord.
A pretty sound, I like it! In equal temperament, this note is at 1000 cents, 18 cents flat of the b7, a clearly audible difference. Here’s the same movie in ET:
Both the b3 and b7 are decidedly flat. The b3 especially sounds different, a lot more dissonant and “beating.”
I wrote a post a while ago, exploring this minor seventh and how it sounds in an untempered chord progression. It’s here.
—————————————-
The next minor seventh is enormously important. This is the dominant-type seventh, b7-, 996 cents. It is fortunate that it is so close to the equal tempered note, 1000 cents, because that means its effect is barely diminished in ET — and it is a really important note in classical music.
The reason it’s called a dominant-type seventh is because it most often shows up with the dominant, or V chord. The note two steps south of the 5 is the 4 — and when you add a 4 to a V chord you get this:
The 4 is a powerful note in this context. It has strong tonal gravity, with reverse polarity. I’ve written several posts about this — here’s one about polarity, here’s one about the use of dominant seventh chords.
Here’s how the chord sounds when it’s built on the 1, in just intonation.
There is strong dissonance when that seventh comes in, and it’s dissonance with a purpose — the chord “wants” badly to resolve somewhere. In this case, it wants to resolve to the 4, the empty space in the middle of the chord. The 1, 3 and 5 are all in the harmonic series of the 4 — that is, they all appear in its “chord of nature,” the overtones that accompany a natural sound. So these notes sort of point to the 4. They point to the 1 even more strongly, though, until that b7- comes into the picture.
When you add the new note, the b7-, something new happens. This note points hard to the 4, and in a different way. It’s as though it says, “home is over there, go!”
Here’s a more detailed discussion.
The entire note collection “wants” to collapse to its center, like a gravitational collapse. The b7- helps to locate that center on the 4.
This effect is often used to move the ear to a IV chord. For example, if you want to start the bridge of a song on the IV, it helps to hit a I7 first. If you’re playing a song in G, and want to go to a C chord, a quick G7 will make the change seem more inevitable. Here’s that move in slo-mo.
The pull of the dominant-seventh-type chord is so strong that it is the sharpest tool in the kit for changing keys, or modulating. Classical composers use it for this constantly.
———————————
The last of the three is a beauty. This is the 7b7, the quintessential note of barbershop harmony, the harmonic seventh, 7/4. The b7- is highly dissonant, the b7 rather neutral, and the 7b7 highly consonant. It sounds (and looks) like this:
This is a resolved chord. In fact, if the consonance and stability of an interval are determined by the smallness of the numbers in its ratio, these are the four most consonant notes of all — 1/1, 3/1, 5/1 and 7/1.
Here is another opportunity to compare just intonation with equal temperament. The harmonic seventh and the dominant seventh sound exactly the same in ET. I believe that a good composer knows, consciously or not, which one is meant.
A good example is the “… and many more” ending so commonly added to Happy Birthday. It is clearly not a dominant type — it’s intended to mean the end of the song, even to put a stronger period on it than the major triad by itself. It’s a quote, or a parody of blues harmony. Play it on the piano and it will be tuned exactly like a I7 chord, but the ear can tell, by context, that there is no move expected, to the IV or anywhere, because it’s heard that little melody a thousand times, and it belongs at the end of a song.
But the signal is so much clearer when the tuning sends the message too! The 7b7 is at 969 cents, a third of a semitone flatter than the piano key.
By the way, I think this is why a common definition of “blue note” is “sung flatter than usual.” I believe the blue notes are the world of multiples of seven, and these just happen to be flatter than the closest notes in the worlds of 3 and 5, the basic lattice.
Here is a video of the 7b7 chord that starts with the harmonic seventh, goes to the equal-tempered seventh, and back to the 7b7.
Quite a difference. ET works because it implies the JI note, and the ear figures out what it’s supposed to be hearing. But the visceral impact is lessened a lot — in this case, IMO, completely.
Nice article! I was wondering if you could go more into mixolydian? Especially when it comes to the minor v chord. In the song “The Only Exception” by Paramore with the chord progression I-v-IV-I would you use the 5- chord on the left side of the lattice then to 4 and have a non-perfect bass movement or use the 5 on the right and go all the way across the lattice to the 4. The song is in B mixolydian and the v chord (F#m) has a minor 7th note(E)over it in the melody which then is resolves down to the tonic (B) and outlines a fourth. If you make the E a 4 note over the minor chord based on 5 it beats with the b7 (A) in the F# minor chord, and if you make E a 4+ it doesn’t outline a perfect fourth when it resolves to the tonic. I’m interested to get your take on how to handle a situation like that. I’ve noticed in mixolydian strange happenings occur when the v chord is used. Like in “Clocks” by Coldplay the higher piano riff that repeats at the end of the song is very consistent like the second hand on a clock in ET, but in JI it has to shift up and down a + to stay in tune depending upon which chord is underneath it.
Hi Zach! I myself would choose the v chord on the right side of the lattice, with the 4 as its 7th. Yes, the 4 beats with the b7, it’s a truly nasty interval, a 4+ or 520 cents, wolfier than anything available in ET. But my ear still reads it all as tension/resolution. When the IV comes around, all is forgiven.
Using the 4+ as the minor seventh of the v leads my ear in the wrong direction. I hear that minor seventh chord as pointing east and south, and I would expect something like a ii chord next. Using the 4 foreshadows the move to the IV, to the west. I’ll want to land hard on the 4 in the bass, and I think a 4+ right before it would weaken the effect.
The v- chord off to the left is a huge harmonic jump, if I really wanted to go there I’d set up for it, visit some other places on the way, it would almost be modulation.
I like to write in the Mixolydian variant that doesn’t have a 5 chord at all, but does have a bVII-. It’s all in one compact area to the left of the lattice, like a major scale but shifted to the left one space. All the intervals work together. In the v version, that poor b7 is all by itself harmonically, and it’s hard to include it in a progression without weird harmonic jumps. The v chord has no neighbors, so it can’t proceed by matchstick harmony.
I’ll go listen to that Coldplay cut, I’m intrigued!
I just spent a fruitful half hour with that Coldplay bit. Very interesting. The chord progression has two bars of v in the middle, and there is some kind of mysterious shift in feeling between the two bars. I can’t hear any actual note change — do you suppose it shifts from a v to a v-? Is that the comma “zap” of ET I’m hearing? The insistent piano notes are the 4 (or 4+) and the 3; the jump from 4+ to 3 is pretty extreme in JI, 4 to 3 makes much more sense, so maybe this is an example of ET teleportation in action. In JI the progression contains a discontinuity, in ET it’s a circle. Thoughts?
Thanks for the reply and the info, what you are saying for The Only Exception definitely makes sense. I unfortunately can’t test out the v- chord because I only have a default JI tuning in my performance editor for my keyboard and I’ve had some trouble getting my H-pi tuning box to work. In the performance editor I can edit the cents for each note but only by whole number amounts and I think certain notes in JI are decimals (like 104.8 cents instead of 104 or 105). Would that matter? Is there somewhere I could find each lattice note in cents value?
In Clocks I hadn’t heard that implied chord change until you had mentioned it. I thought originally it was I to v to ii- but I forgot that v to ii- might sound weird. Trying to figure things out in JI can be like solving a Sudoku puzzle sometimes, only a lot more fun and rewarding lol. I think you may have something with the v to v- movement. In terms of the piano riff at the end, I would be interested to hear 4 and 3 over the I and 4+ and 3+ over the v, then back to 4 and 3 for the last two chords. That would lessen the distance between the 4+ and 3. The note in the riff that comes after the 3 or 3+ would either be the b7 or the b7- so it would be dissonant anyway. Only because that 4 and b7 together on beat one of the v chord, and every accented beat that measure, just sounds so gnarly. What do you think? Or does the song just not work in JI? I feel like if there is a will, there is a way. I do find it interesting though that the song is called Clocks and the piano riff is definitely reminiscent of the “evenly spaced” seconds on a ticking clock, which not only hints at its consistency of rhythm but seemingly to its harmonic nature as well.
I love the song Clocks but something tells me, considering it was written in something like 10 min by playing random notes on the piano, that if it wasn’t for ET, this song would have never happened, lol. I guess ET does have some fruits after all. Then they can leave it to guys like you and me to figure out how to play it in JI, lol.
Wow great stuff. I have to take off for the weekend but I’ll respond more next week. ET does have tricks up its sleeve that can’t be done in JI, apparently people have tried hard to port Beethoven over into JI and just can’t do it. I had that thought about Clocks too, it may be a demo of the special powers of ET.
Also: I’ve found that whole cents are plenty close enough. To calculate cents from the note’s ratio: 1200 x log2(ratio). Make sure the ratio is octave-reduced so its value is between 1 and 2. I use Logic, which allows entering the ratio directly into a tuning table — very handy. You only get a 12-note palette, so if you want more you have to switch tuning tables.
OK Zach, some more thoughts. I like the Sudoku reference; the lattice also feels to me like chess, with different pieces that have different moves. The bass likes to move slowly, by small harmonic distances, other voices move faster and further, and the melody is the Queen, she can do anything.
So dissonances should perhaps be most present in the faster-moving, “lighter” voices. And as you mention, they’ll work better on the weak beats.
That said, what is that energy shift between the 2d and 3rd bar, both v chords? Maybe it’s a full-chord comma, everything swoops across the lattice, ET teleportation.
Good to be trading ideas.
Gary,
I’m really digging the work. Fantastic stuff. This lattice paradigm is quite fun lookin. I’m curious to run it through Hindemith’s Interval Theory (http://www-pub.naz.edu/~jturner9/EZGuideExpSyl.html) and see what comes out!
I’m also curious to hit it up against Barry Harris’ 6th diminished theory (If you’re not familiar with it, here’s a synthesis of it that I like: https://www.youtube.com/watch?v=AF67azWnMvw&😉
I’m also curious what the lattice would look like drawn in 3 dimensions. Is that really where the b3, b5, and b7 are? Raised up a bit, adding that difficult to render 3rd dimension of “depth”. Funny how they’re all blue notes too. Hmmmm.
Hi Sonny — I do think of the septimal intervals as being in a third dimension. The three axes would be x3, x5 and x7 (harmonic steps of a fifth, a major third, and a harmonic seventh). The notes generated on the “7” axis are blue notes (7b3, 7b5, 7b7), but the regular minor notes (b3, b5, b7), are generated by compounding fifths and major thirds. The blue notes are way flatter than the minors. Good luck mining Hindemith and Harris! I hadn’t heard of Harris’ work. Do read Mathieu if you can. Thanks! Gary
Cool article. In a similar manner, have you noticed that the perfect fourth often ends up functioning as 21:16 instead of 4:3? This is especially pronounced in mixolydian, which sounds very “septimal” imo. To me, mixolydian plays modally as:
C: 1/1
D: 9/8
E: 5/4
F: 21/16
G: 3/2
A: 27/16
Bb: 7/4
I have not noticed this! Are you using it as a melody note? Over what chords does it sound best?